


Geo.M.G.GPE.B.07: The Highly Proficient student can use coordinates to find the perimeter of polygons and area of triangles and rectangles, and apply them to real-world problems.

Geo.M.G.GPE.B.05: The Highly Proficient student can create the equation of a line parallel or perpendicular to a given line that passes through a given point in a context. Geo.M.G.CO.D.13: The Highly Proficient student can construct an equilateral triangle, a square, and a regular hexagon inscribed in a circle with a variety of tools and methods. Geo.M.G.CO.D.12: The Highly Proficient student can construct various geometric objects using a variety of tools and methods.
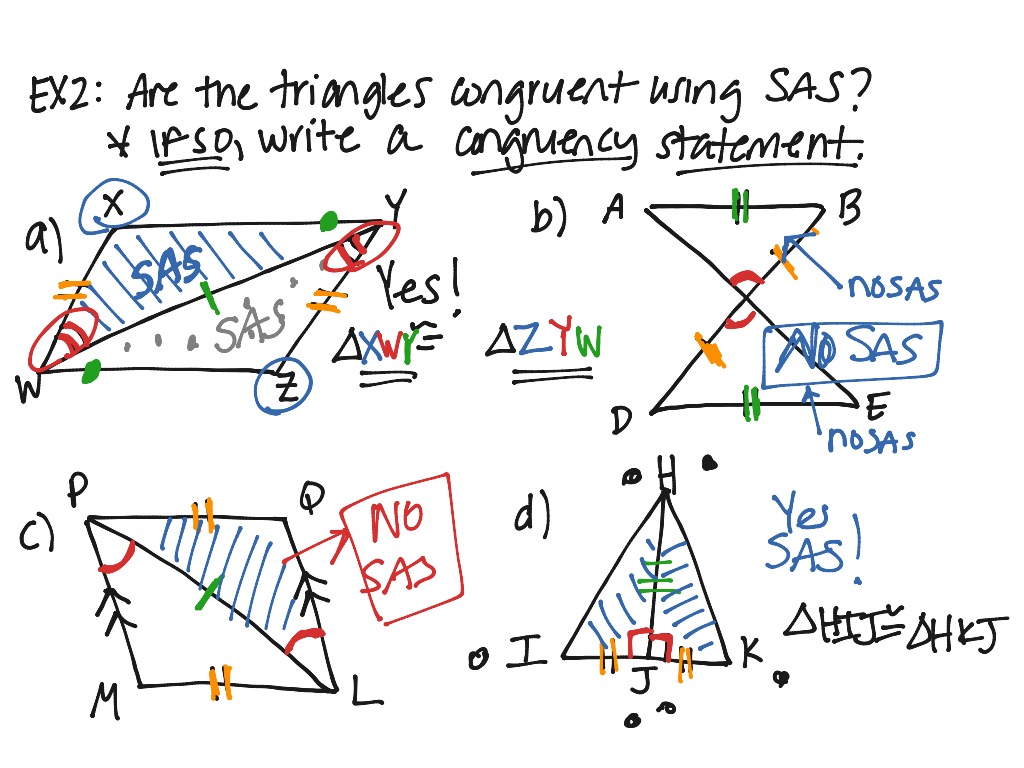
Geo.M.G.CO.C.09: The Highly Proficient student can prove theorems such as: alternate interior angles are congruent vertical angles are congruent consecutive interior angles are supplementary and apply theorems in real-world context.
#Ssa hs sas geometry definition series
Geo.M.G.CO.A.05: The Highly Proficient student can perform 2 or more transformations on a figure, identify the single or series of transformations that map a pre-image to an image, and explain how the order of a sequence of transformations being performed may result in different outcomes. Geo.M.G.CO.A.04: The Highly Proficient student can represent functions to describe transformations using a variety of media and justify statements about rotations, reflections, and translations on the coordinate plane. Geo.M.G.CO.A.03: Given a rectangle, parallelogram, trapezoid, or regular polygons, the Highly Proficient student can describe the rotations and reflections that carry it onto itself. Compare transformations that preserve distance and angle to those that do not. Geo.M.G.CO.A.02: The Highly Proficient student can represent and describe transformations in the plane as functions that take points in the plane as inputs and give other points as outputs. That's all you need to know and you can say that these two triangles must be .G.CO.A.01: The Highly Proficient student can explain the definition of an angle, circle, perpendicular lines, parallel lines and identify real-world examples of each figure. These are both angle angle side, angle angle side. The side that I know has to be non included so could be over there or it could also be on the other side. All you need to know are these 3 items and you can say yes these two triangles must be congruent.īut there's one other one that we're going to talk about and that is angle angle side so I'm going to erase these markings just so we can draw our comparison, so angle angle side says that if you know about these two triangles are two angles and a non included side so what's difference about this is I could say that these two angles are congruent but the side that I know is not in between the two angles. One shortcut is angle side angle, so what does that mean angle side angle? Well what it means is if you have one triangle and I tell you that these two corresponding angles are congruent, and if an included side is congruent, well what do I mean by included? Well I mean that this other angle here that is adjacent to that side that these two angles must be congruent so I know an angle I have the side and an angle so that is called the angle side angle shortcut. What are they? Basically when you have two different triangles and you're trying to determine are the 3 angles of these two triangles congruent? And are the 3 sides congruent? We don't need to know all 6 items.


 0 kommentar(er)
0 kommentar(er)
